锁模（Mode Locking）

定义：激光器产生超短脉冲采用的技术。

锁模是一种激光器产生超短脉冲的方法（实际上是一组方法），然后这种激光器就被称为锁模激光器。其中，激光谐振腔中包含一种有源组件（光调制器）或者无源非线性器件（饱和吸收器），从而光能够在谐振腔中循环往复形成超短脉冲。在稳态情况下，影响循环脉冲的各种效应达到平衡，脉冲每循环一周后参数不会发生变化，或者几乎不发生变化。而每当脉冲入射到输出耦合器的反射镜上时，就会辐射一个可用的脉冲，其重复周期对应于谐振腔中循环一周所需的时间（通常为几个纳秒），脉冲长度非常短；通常在30fs到ps之间，极限情况下可以低至5fs。因此，锁模激光器的峰值功率会比其平均功率高几个数量级。

本词条侧重于描述锁模的方法和一些基本原理，在锁模激光器词条中则包含各种锁模激光器更多的细节。

图1：无源锁模激光器中产生脉冲列的过程。介质中的增益补偿损耗，饱和吸收反射镜会增强脉冲产生过程。每次脉冲入射到输出耦合反射镜，就会有一个脉冲产生。

主动和被动锁模

主动锁模需要周期性调制谐振腔损耗或者循环一周的相位变化，通常是由声光调制器、电光调制器、马赫-曾德尔集成光学调制器或者半导体电吸收调制器来实现。周期性调制结合谐振腔就可以得到超短脉冲，通常长度为皮秒。大多数情况下，得到的脉冲长度是由调制器引起的脉冲压缩和其它效应（例如有限的增益带宽）引起的脉冲展宽之间的平衡来决定的。

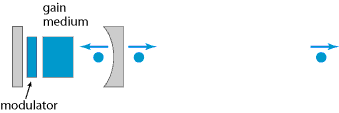
图2：主动锁模激光器装置示意图。

被动锁模（采用饱和吸收器）可以产生更短的脉冲（飞秒），主要是因为饱和吸收器本身是由短脉冲驱动的，比电子调制器调制谐振腔损耗更快：脉冲越短，损耗调制越快，前提是吸收器的恢复时间足够短。脉冲长度甚至会小于吸收器的恢复时间。有些情况下，并不能达到快速锁模。

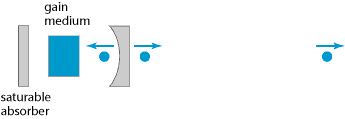
图3：被动锁模激光器示意图。

在主动锁模和被动锁模词条中有更详细的介绍。

在有些激光器中（尤其是锁模二极管激光器），需要同时采用主动和被动锁模。这种混合锁模激光器结合了一些关键的优势，例如外加控制脉冲重复频率和较短脉冲。

连续光与同步泵浦对比

大多数锁模激光器是连续光泵浦的，通常采用激光二极管。泵浦光源为增益介质提供连续的光源，而循环的脉冲以规律的时间间隔提取出能量。大多数情况下，与上能态寿命相比，脉冲间隔较短，因此在这一时间内增益介质可以非常容易的储存能量。那么采用相同的平均功率的连续光激光器，增益饱和情况相同。

即使有些增益介质具有相对较短的上能态寿命，例如在染料激光器或者一些半导体激光器中，连续光泵浦时可能的，前提是脉冲重复频率不能太低。如果不能满足这一条件，单脉冲引起的增益饱和效应很强（脉冲形成过程就会不稳定），可以采用同步泵浦方法。但是，这就需要另外一个锁模激光器作为泵浦源。

高脉冲重复频率和低脉冲重复频率

高的脉冲重复频率通常是由谐波锁模得到的，其中多个脉冲以恒定的时间间隔在谐振腔中循环往复。这样即使采用光纤激光器也可以产生几个GHz的脉冲列，往返一周频率只有几十个MHz。

采用基本锁模得到的高脉冲重复频率的情况下，即不采用谐波锁模，需要非常短的激光谐振腔。如果通过适当的设计，那么可以避免Q开关不稳定性，这种激光器就会非常简单，稳定且体积小。

在脉冲重复频率很高时，锁模激光器得到的脉冲能量非常有限，通常为纳焦耳或者皮焦耳。采用倾斜腔锁模激光器和正反馈放大器，就能同时获得很高的脉冲能量和更低的重复频率。

光谱：频率梳

锁模激光器产生脉冲列的光谱并不是平滑的，而是包含等间距的分离的线，间距与脉冲重复速率相等（参阅频率梳）。尽管谐振腔模式的谐振频率并不总是等间距的也会得到频率梳，因为增益介质中的色散效应的存在：锁模机制使激光器产生光的频率域谐振腔模式的频率不相等。这种频率差值可能非常高，只有当谐振腔色散非常小时才能够得到宽谱，这样谐振腔模式的频率近似是相等的。在时间域，可以理解为色散造成时间谱展宽，需要采用锁模机制进行补偿。然而需要注意的是，光学非线性效应也可能比较强，因此考虑“冷腔模式”会忽略很重要的一部分物理机制。

“锁模”的起源

锁模的名称来自于频域的一种描述：当激光谐振腔中的纵模之间具有固定相位关系时形成超短脉冲，更准确的说，是激光输出光谱的线之间。然而，锁模的基本机制在时间域上更容易理解。并且，在强的光学非线性效应影响下，谐振腔模式的概念就存在疑问。严格说来，不建议把锁模激光器光谱中的线称为模式，尽管光谱中分立的线与谐振腔模式是有关系的。

可以将周期性脉冲列的合成看做一系列叠加等频率间隔的正弦振荡（图4）（对应于锁模激光器不同的轴向谐振腔模式）的叠加。采用的频率组分越多，产生脉冲的长度越短。

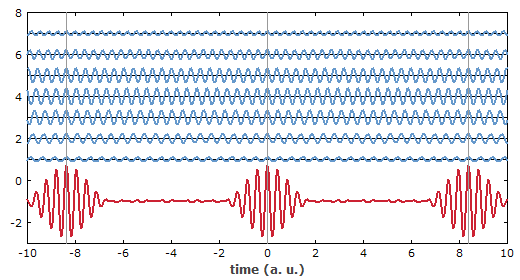
图4：通过叠加七个不同模式的正弦波（蓝色曲线）合成的周期性脉冲列（红色曲线）。竖直线表示所有同相位的振荡对应的时间点。

一个很重要的因素在于这些谐振腔模式需要具有固定的相位关系。如图5所示：蓝色曲线表示脉冲列具有固定的相位关系，因此在某个时间点，各频率组分的电场叠加得到总的场强度为最大值。红色曲线表示具有相同强度的各频率组分的电场，但是具有随机的相对相位。

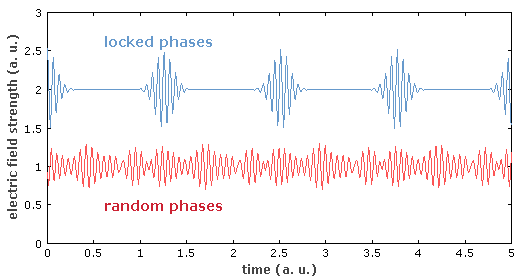
图5：激光腔内电场的时间演化曲线，蓝色曲线是模式间具有固定的相位关系，红色曲线对应模式的相位差是随机的。

锁模激光器的不稳定性和噪声

锁模激光器采用的不同机制会产生各种不稳定性。例如，激光器可能产生不稳定间隔的多个脉冲，不稳定能量的脉冲，或者具有本地噪声的脉冲。在追溯这些问题起因时采用的不同的模型非常重要，然后再寻找合适的解决方法。

即使不存在常规的不稳定性因素，锁模激光器的输出也包含各种噪声；通常需要特别注意的是时间抖动（脉冲位置的随机涨落）。其它的噪声包括相位噪声，强度噪声，以及脉冲长度，啁啾和中心频率的涨落。相位噪声导致产生的频率梳的有限展宽。锁模激光器中的不同类型的噪声具有很多联系[16]。

需要注意的是，锁模激光器词条中包含更多不同锁模激光器的细节描述，在主动锁模和被动锁模词条中则对锁模技术有很详细的描述。

参考文献

[1] W. E. Lamb Jr., “Theory of an optical laser”, Phys. Rev. 134 (6A), A1429 (1964) (proposed the technique of mode locking)

[2] L. E. Hargrove, R. L. Fork, and M. A. Pollack, “Locking of He–Ne laser modes induced by synchronous intracavity modulation”, Appl. Phys. Lett. 5, 4 (1964) (first report of active mode locking)

[3] M. DiDomenico, “Small-signal analysis of internal (coupling type) modulation of lasers”, J. Appl. Phys. 35 (10), 2870 (1964)

[4] D. J. Kuizenga and A. E. Siegman, “FM and AM mode locking of the homogeneous laser – Part I: theory”, IEEE J. Quantum Electron. 6 (11), 694 (1970)

[5] E. P. Ippen, C. V. Shank, and A. Dienes, “Passive mode locking of the cw dye laser”, Appl. Phys. Lett. 21, 348 (1972) (first continuous-wave mode locking with a saturable absorber)

[6] B. K. Garside and T. K. Lim, “Laser mode locking using saturable absorbers”, J. Appl. Phys. 44 (5), 2335 (1973)

[7] G. H. C. New, “Pulse evolution in mode-locked quasi-continuous lasers”, IEEE J. Quantum Electron. 10 (2), 115 (1974)

[8] L. F. Mollenauer and R. H. Stolen, “Soliton laser”, Opt. Lett. 9 (1), 13 (1984)

[9] J. G. Fujimoto, A. M. Weiner, and E. P. Ippen, “Generation and measurement of optical pulses as short as 16 fs”, Appl. Phys. Lett. 44, 832 (1984)

[10] R. L. Fork et al., “Compression of optical pulses to six femtoseconds by using cubic phase compensation”, Opt. Lett. 12 (7), 483 (1987)

[11] H. A. Haus, “Mode-locking of lasers”, IEEE J. Sel. Top. Quantum Electron. 6 (6), 1173 (2000)

[12] R. Paschotta, “Passive mode locking with slow saturable absorbers”, Appl. Phys. B 73 (7), 653 (2001)

[13] R. Paschotta et al., “Soliton-like pulse shaping mechanism in passively mode-locked surface-emitting semiconductor lasers”, Appl. Phys. B 75, 445 (2002)

[14] R. Paschotta, “Noise of mode-locked lasers. Part I: numerical model”, Appl. Phys. B 79, 153 (2004); R. Paschotta, “Noise of mode-locked lasers. Part II: timing jitter and other fluctuations”, Appl. Phys. B 79, 163 (2004)

[15] N. Usechak and G. Agrawal, “Semi-analytic technique for analyzing mode-locked lasers”, Opt. Express 13 (6), 2075 (2005)

[16] R. Paschotta et al., “Optical phase noise and carrier–envelope offset noise of mode-locked lasers”, Appl. Phys. B 82 (2), 265 (2006)

[17] R. Paschotta and U. Keller, “Passively mode-locked solid-state lasers”, in Solid-State Lasers and Applications (ed. A. Sennaroglu), CRC Press, Boca Raton, FL (2007), Chapter 7, pp. 259–318

[18] R. Paschotta, Field Guide to Laser Pulse Generation, SPIE Press, Bellingham, WA (2007)

[19] R. Paschotta, case study on active mode locking

[20] R. Paschotta, case study on passive mode locking